最近有个小朋友问我Dandelin用来证明一个平面截圆锥得到的截口曲线是椭圆的模型的题咋做的，我一看，我大意了，不会做…
所以直接去网上百度一下，水了一篇博客出来
0x01 Dandelin模型
你是否在寻找Dandelion()
Germinal Dandelin，著名数学家，主要成就有Dandelin双球模型，在圆锥与圆的切线等研究上取得了巨大的成果。其Dandelin的双球模型便是在一个圆锥内塞入两个球，这两个球既与圆锥相内切，又与一个公共平面相切，这个公共平面截圆锥所得到的截口曲线便是圆锥曲线（可以是椭圆、双曲线和抛物线）
0x02 Dandelin双球模型的证明
根据圆锥曲线的第一定义即可证明：
如果平面内一动点与两定点F1、F2的距离之和等于一个常数的轨迹为椭圆
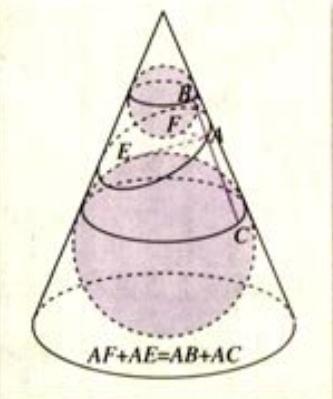
那么我们就有如下的证明过程，假设上面的小圆圆心为O1、大圆圆心为O2，内切球与圆锥的交点为B、C：
所以截口曲线便是椭圆
0x03 截口曲线离心率的计算
离心率计算公式：
那么我们根据几何关系计算出c和a即可
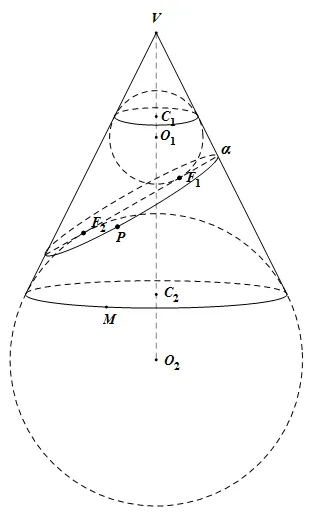
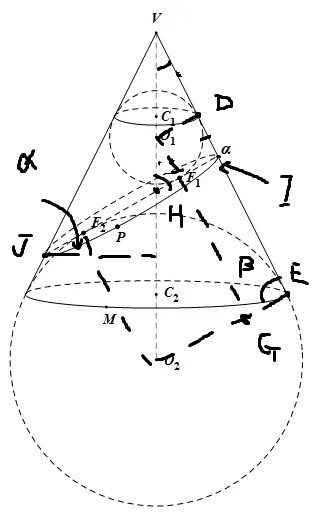
为方便计算取其截面图如上，并且添加辅助线后的图如下（辅助线是手动添加的，可能十分不平整）：
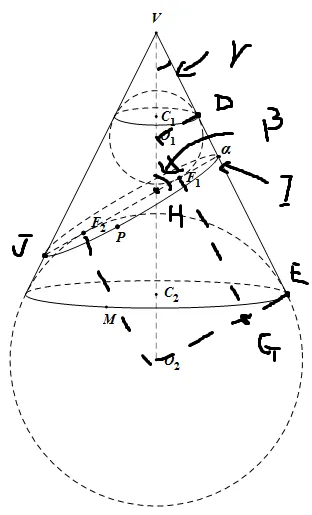
假设D、E是切点，连接O1F1、O2F2、O1D、O2E
又作O1G垂直于O2E，垂足为G（O1、F1、G三点并不共线）
同时设轴线C1C2与平面α的交点为H 夹角为β、与母线的夹角为γ
由上面的推导可得到：
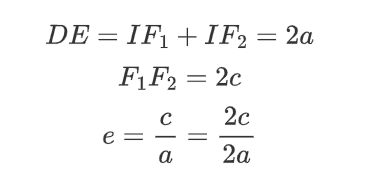
容易证明得到：
就能够将DE转到O1G
接下来提供两种方法（其实二者是一致，实际上只有一种的）：
（假设圆的半径，O1O2的距离已知）
法一：
其实细细看来可以进行如下的推导：
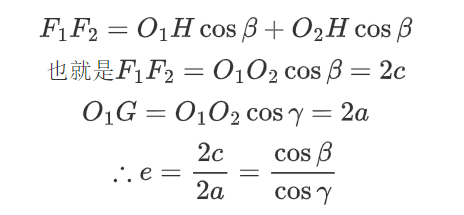
这也就是方法二，计算这两个夹角的余弦值即可
其实这两个方法确实是一样的（雾
当然，如果选取的夹角不一样，得到的结论也会略有不同，但是离心率的值仍然是两个角度的比值：
参考了闲敲棋子落灯hua师傅的文章
0x04 小拓展
由该双球模型得出的离心率的取值是由截面与底面的夹角α决定的（一般认为圆锥固定不变）
所以截取的角度不同，所得到的圆锥曲线也不同（根据离心率判断即可）
在某些动点类求轨迹的问题中，也可以通过截面与底面的夹角α，母线与底面的夹角β来确定离心率，从而确定轨迹是何种圆锥曲线
更多的题型可以去参考棋子落灯hua师傅的文章，由于本人能力有限，这里就不作展开
其实真的是因为我又菜又懒，然后啥也不会...
参考文章：